> 2021年04月12日信息消化 ### 每天学点机器学习 #### 多元线性回归 Multivariate Linear Regression ##### 多变量的梯度下降 Gradient Descent for Multiple Variables 下图是一个变量的梯度下降和多个变量的梯度下降的比较。 > The following image compares gradient descent with one variable to gradient descent with multiple variables: 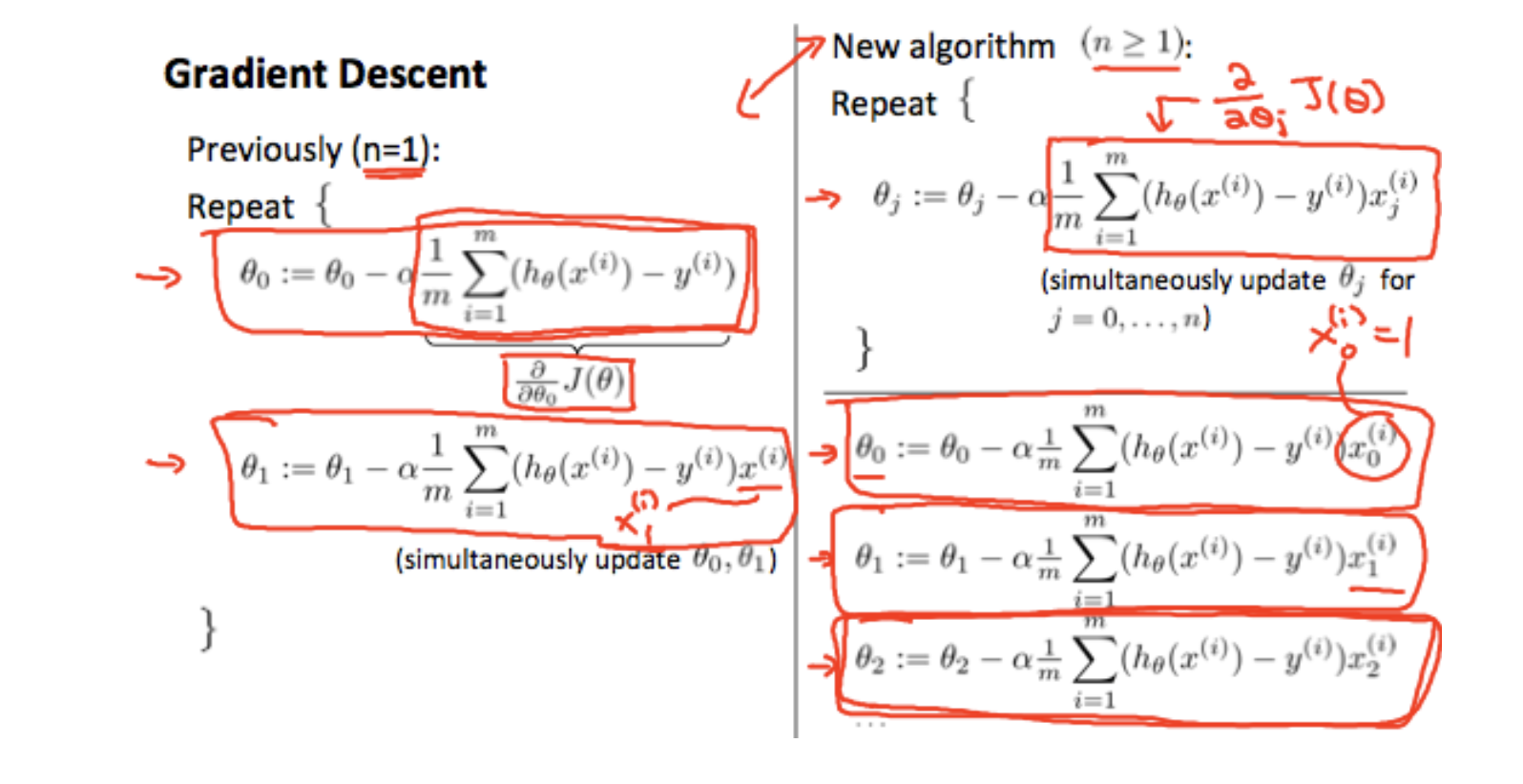 ##### 特征缩放和平均归一化 Feature Scaling and Mean Normalizations 我们可以通过让每个输入值都在大致相同的范围内来加快梯度下降的速度。这是因为θ在小的范围内下降得很快，而在大的范围内下降得很慢，所以当变量非常不均匀时，会低效率地振荡下降到最优值。 > We can speed up gradient descent by having each of our input values in roughly the same range. This is because θ will descend quickly on small ranges and slowly on large ranges, and so will oscillate inefficiently down to the optimum when the variables are very uneven. 防止这种情况发生的方法是修改我们输入变量的范围，使它们都大致相同。最理想的情况是: > The way to prevent this is to modify the ranges of our input variables so that they are all roughly the same. Ideally: $−1 ≤ x_{(i)} ≤ 1$ 或者 $−0.5 ≤ x_{(i)} ≤ 0.5$ 两种有助于解决这个问题的技术是特征缩放和平均标准化。特征缩放是将输入值除以输入变量的范围（即最大值减去最小值），结果新的范围只有1。平均归一化是将输入变量的平均值从该输入变量的值中减去，结果新的输入变量平均值只有0。 > Two techniques to help with this are **feature scaling** and **mean normalization**. Feature scaling involves dividing the input values by the range (i.e. the maximum value minus the minimum value) of the input variable, resulting in a new range of just 1. Mean normalization involves subtracting the average value for an input variable from the values for that input variable resulting in a new average value for the input variable of just zero. $x_i=\frac{x_i - μ_i}{s_i}$ $μ_i$是特征(i)的所有值的平均值，$s_i$是数值范围(最大值-最小值) 或者说$s_i$ 是标准差。 Where $μ_i$ is the **average** of all the values for feature (i) and $s_i$is the range of values (max - min), or $s_i$ is the standard deviation. ##### 学习率 Learning Rate 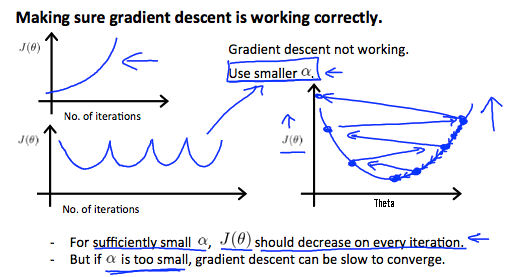 总结一下。 如果α太小： 收敛速度慢。 如果α太大: 可能不会在每次迭代中减少(overshooting)，因此可能不会收敛。 > If α is too small: slow convergence. > > If α is too large: may not decrease on every iteration and thus may not converge. ##### 特征和多项式回归 Features and Polynomial Regression 我们可以通过几种不同的方式改进我们的特征和假设函数的形式。 我们可以**将多个特征合并**为一个特征。例如，我们可以将$x_1$和$x_2$合并成一个新的特征$x_3$，取$x_1⋅x_2$。 We can improve our features and the form of our hypothesis function in a couple different ways. We can **combine** multiple features into one. For example, we can combine $x_1$ and $x_2$ into a new feature $x_3$ by taking $x_1⋅x_2$ ##### 正态方程 Normal Equation $\theta = (X^TX)^{-1}X^Ty$ $(X^TX)^{-1}$ is inverse of matrix $X^TX$ Octave: `pinv(x'*x)*x'*y` ##### 梯度下降 vs 正态方程 | Gradient Descent | Normal Equation | | :------------------------- | :------------------------------------------------------ | | Need to choose alpha | No need to choose alpha | | Needs many iterations | No need to iterate | | O (kn^2*k**n*2) | O (n^3*n*3), need to calculate inverse of X^TX*X**T**X* | | Works well when n is large | Slow if n is very large | ##### 随堂小测1 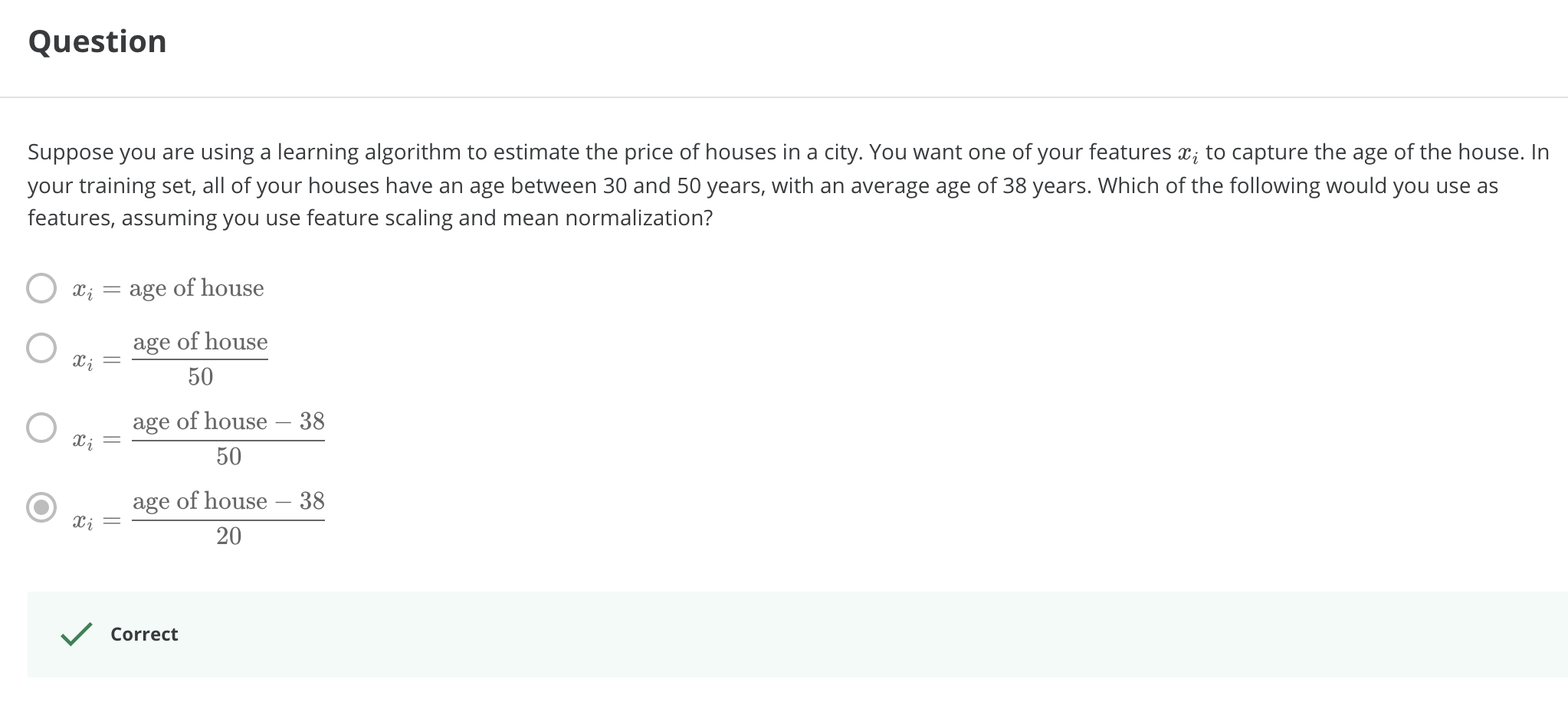 ##### 随堂小测2 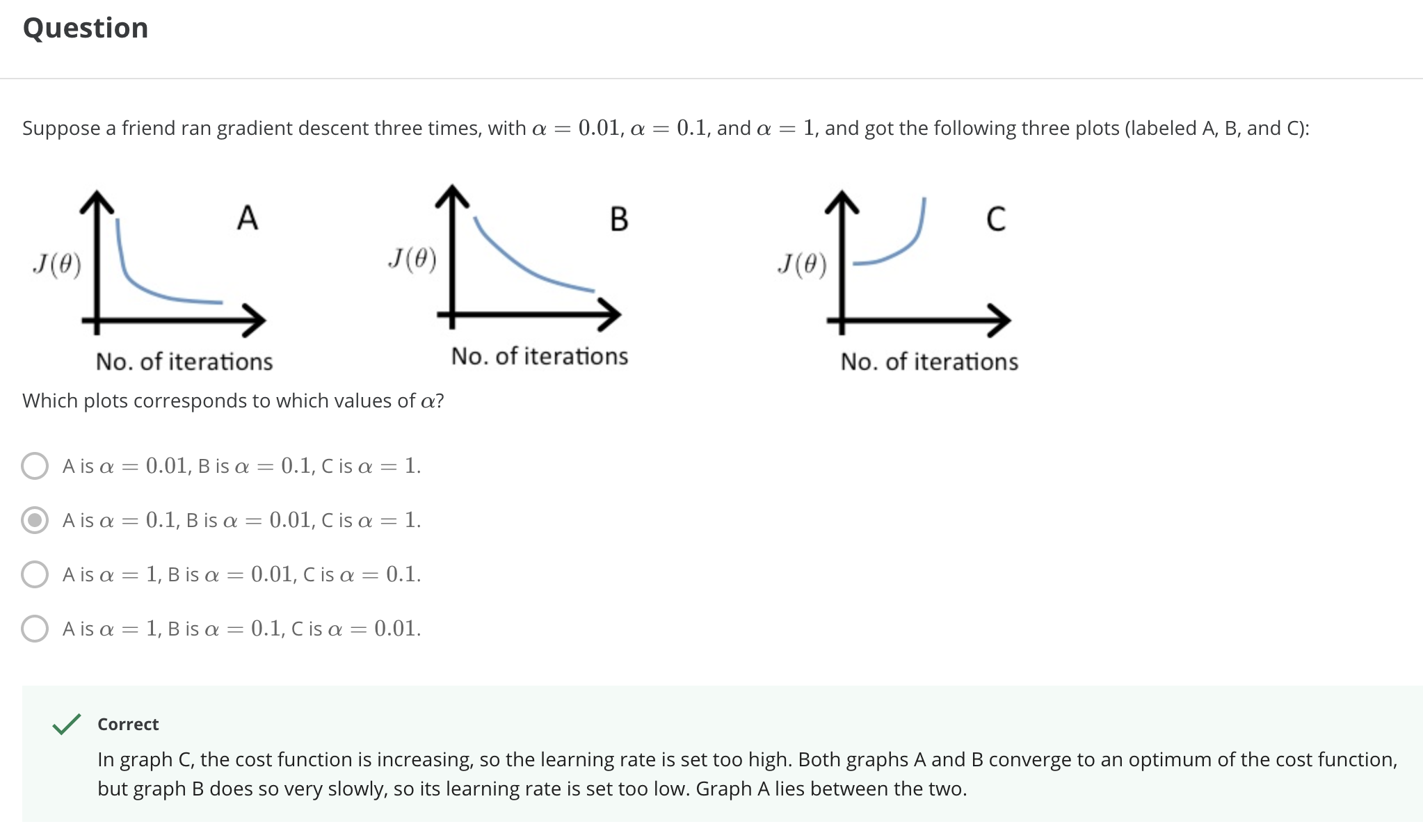 ##### 随堂小测3 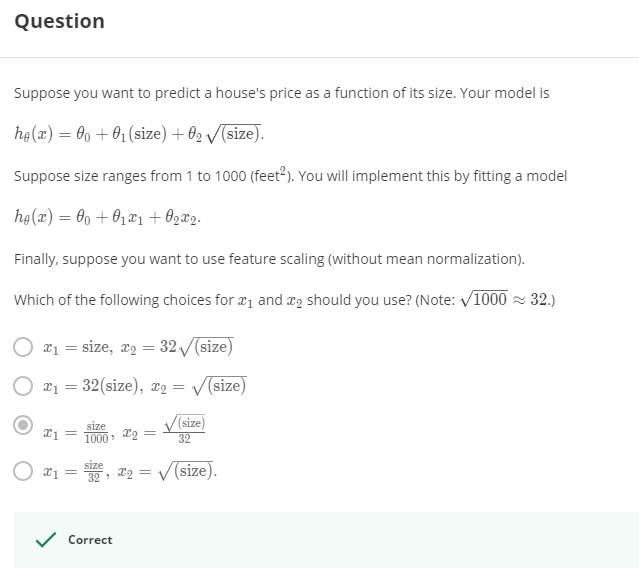 ### 其他值得阅读 #### 3个极简主义习惯让我的生活得到极大改善 原文：[3 Minimalist Habits That Improved My Life Immensely](https://medium.com/alyssas-healthy-tidbits/3-minimalist-habits-that-improved-my-life-immensely-db60441af2f7) - 每隔三到六个月，扔掉不要的衣服。 - 要养成用心购买的习惯 - Will this purchase help me in some way? Will this purchase make me happy? Is this item something I have been wanting for a while? Is it unlike anything I already own? - 这次购买对我有什么帮助吗？ 这次购买会让我开心吗？ 这件东西是我一直想要的东西吗？ 它和我已经拥有的东西不一样吗？ - 每天打扫（尤其桌面），保持干净整洁。 > "我们的物理环境会极大地影响我们的认知、情绪和行为，影响我们的决策和与他人的关系。杂乱无章的空间会对我们的压力和焦虑水平，以及我们的专注力、饮食选择，甚至是睡眠产生负面影响。" > “Our physical environments significantly influence our cognition, emotions, and behavior, affecting our decision-making and relationships with others. Cluttered spaces can have negative effects on our stress and anxiety levels, as well as our ability to focus, our eating choices, and even our sleep.” #### 一人公司方法论 原文：https://github.com/easychen/one-person-businesses-methodology ##### 矛盾和解决 这里就出现了一个非常明显的矛盾：一方面是我们个人的时间精力非常有限（一周就50~60个小时）；另外一方面，我们又有非常大量的事情要做，因为公司就我们一个人，所有的事情都是要有人来做的。 ##### 提升效率 第一个方向，一个人的时间和精力是有限的，那我们能不能提升效率。 这个对于其他的行业来讲，可能会比较难，但是对于程序员来讲，可以考虑自动化和人工智能。如果在这两个方向上有突破的话，我们就可以把个人的时间和精力从重复劳动里面解放出来，让机器高效率的去处理重复的事情，把我们仅有的精力放到创造性的、开创性的业务上面来。 ##### 定向投放 除了通用渠道，我们还可以考虑做定向投放。所谓定向投放是说，对这个小众市场的行业网站和社区投放广告，或者向这个小众市场相关的意见领袖（KOL）做营销推广，再或者购买搜索关键字来导流。这部分的效果会好一些，但成本就要看这个行业竞争如何了，竞争激烈的比通用渠道投放还要贵。 ##### 分离非核心业务 确定了市场以后，我们还可以对自己的业务进行取舍。比如，我们把非核心业务给分离出来。这些业务，我们可以外包、可以兼职。对于一些基础设施，我们可以「以租代建」。 ##### 实际操作 前面说了这么多的分析，但离落地还有一点点距离。在最后一部分里，我们就来思考下怎么落地。 1. 发现一个趋势 2. 寻找一个小市场 3. 针对这个市场 1. 面向 1000 个用户，提供一个每月 50 元定价的产品 2. 或者面向 10000 个用户，提供一个每月 5 元的产品 4. 开发产品并持续运营 关于趋势发现，简单粗暴的方式是读研究报告。比如[艾瑞网](http://www.iresearch.com.cn/report.shtml)会定期更新一些简版报告，从里边的数据可以发现很多有意思的趋势。不过这些报告更多的是面向创业投资领域，未必适合一人公司。像我经常在微博上提到的 [Trende.vc](https://weibo.com/ttarticle/p/show?id=2309404559878248333577) 这种专门为独立开发者和一人公司准备的分析报告，就更有针对性一些。 ### 一点收获 - 简单用Nuxtjs做了一个预约表。因为是用 codeSandbox 模版直接做的开发，把代码同步到 github，再回到 codeSandbox 做修改居然要fork, 看了下[文档](https://codesandbox.io/docs/git)，原来 GitHub sandboxes 是 immutable 的, 这里在 fork 的 sandbox 里找到 Github 的 tab 然后点击 Link Sandbox 的按键就可以直接commit到Github仓库里。 记录下Netlify部署的配置 - 首先是nuxt config，配置只渲染客户端。 ``` buildDir: 'dist', target: 'static', ssr: false, ``` - Netlify配置 - Build command： npm run generate - Publish directory： dist/