> 2021年06月21日信息消化 ### 每天学点Golang ### 每天学点机器学习 #### Implementation Note: Unrolling Parameters https://www.coursera.org/learn/machine-learning/lecture/60Uxp/implementation-note-unrolling-parameters With neural networks, we are working with sets of matrices: $$ Θ(1),Θ(2),Θ(3),…\\D(1),D(2),D(3),… $$ In order to use optimizing functions such as "fminunc()", we will want to "unroll" all the elements and put them into one long vector: ```matlab thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ] deltaVector = [ D1(:); D2(:); D3(:) ] ``` If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11, then we can get back our original matrices from the "unrolled" versions as follows: ```matlab Theta1 = reshape(thetaVector(1:110),10,11) Theta2 = reshape(thetaVector(111:220),10,11) Theta3 = reshape(thetaVector(221:231),1,11) ``` To summarize:  ##### 随堂小测 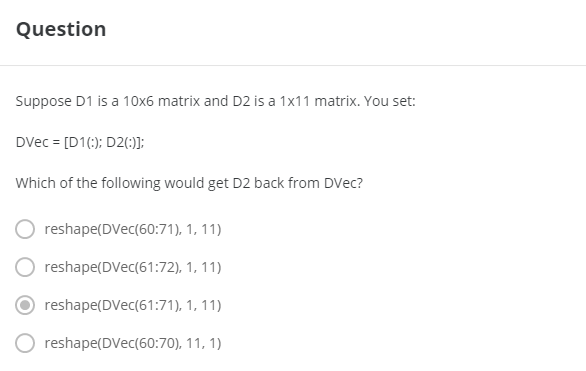 #### Gradient Checking Gradient checking will assure that our backpropagation works as intended. We can approximate the derivative of our cost function with: $$ \dfrac{\partial}{\partial\Theta}J(\Theta) \approx \dfrac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2\epsilon} $$ With multiple theta matrices, we can approximate the derivative **with respect to** $Θ_j$ as follows: $$ \frac{∂}{∂Θ_j}J(Θ)≈\frac{J(Θ_1,…,Θ_j+ϵ,…,Θ_n)−J(Θ_1,…,Θ_j−ϵ,…,Θ_n) }{2ϵ} $$ A small value for *ϵ* (epsilon) such as ${\epsilon = 10^{-4}}$$, guarantees that the math works out properly. If the value for \epsilon*ϵ* is too small, we can end up with numerical problems. Hence, we are only adding or subtracting epsilon to the $\Theta_j$ matrix. In octave we can do it as follows: ```octave epsilon = 1e-4; for i = 1:n, thetaPlus = theta; thetaPlus(i) += epsilon; thetaMinus = theta; thetaMinus(i) -= epsilon; gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon) end; ``` We previously saw how to calculate the deltaVector. So once we compute our gradApprox vector, we can check that gradApprox ≈ deltaVector. **Once you have verified once that your backpropagation algorithm is correct, you don't need to compute gradApprox again. The code to compute gradApprox can be very slow.** ##### 随堂小测   #### Random Initialization Initializing all theta weights to zero does not work with neural networks. When we backpropagate, all nodes will update to the same value repeatedly. Instead we can randomly initialize our weights for our Θ matrices using the following method: 将所有Theta权重初始化为零对神经网络不起作用。当我们反向传播时，所有节点都会重复更新到相同的值。相反，我们可以用以下方法随机初始化我们的Θ矩阵的权重;  Hence, we initialize each $\Theta^{(l)}_{ij}$ to a random value between[−ϵ,ϵ]. Using the above formula guarantees that we get the desired bound. The same procedure applies to all the Θ's. Below is some working code you could use to experiment. ```octave If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11. Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON; Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON; Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON; ``` rand(x,y) is just a function in octave that will initialize a matrix of random real numbers between 0 and 1. (Note: the epsilon used above is unrelated to the epsilon from Gradient Checking) ###### 随堂小测  ##### Putting It Together First, pick a network architecture; choose the layout of your neural network, including how many hidden units in each layer and how many layers in total you want to have. - Number of input units = dimension of features x^{(i)}*x*(*i*) - Number of output units = number of classes - Number of hidden units per layer = usually more the better (must balance with cost of computation as it increases with more hidden units) - Defaults: 1 hidden layer. If you have more than 1 hidden layer, then it is recommended that you have the same number of units in every hidden layer. **Training a Neural Network** 1. Randomly initialize the weights. 2. Implement forward propagation to get $h_\theta(x^{(i)})$ for any $x^{(i)}$ 3. Implement the cost function 4. Implement backpropagtion to compute partial derivatives. 5. Use gradient checking to confirm that your backpropogation works. Then diable gradient checking. 6. Use gradient descent or a built-in optimization functino to minimize the cost function with weights in theta. When we perform forward and back propagation, we loop on every training example: ```octave for i = 1:m, Perform forward propagation and backpropagation using example (x(i),y(i)) (Get activations a(l) and delta terms d(l) for l = 2,...., L) ``` 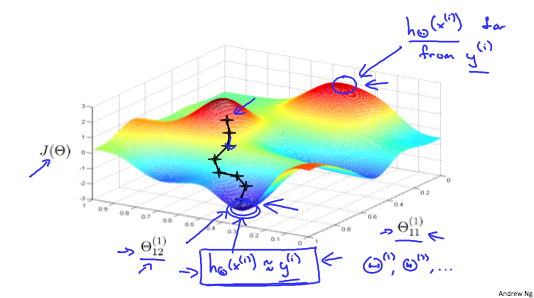 Idealy, you want $h_\theta(x^{(i)}) ≈ y^{(i)}$. This will minimize our cost function. However, keep in mind that $J(\theta)$ is not convex and thus we can end up in a local minimum instead.  ### 其他值得阅读 #### Lesson 7: Modular scale & meaningful typography ##### Using a modular scale ###### 1 Choose your base size Once you decided what typeface to use for your main body you need to find out what size works best. As we’ve seen before, not all typefaces sizes are equal. Some seem taller or bigger, some shorter and lighter. Put it in your browser and experiment with the size, line-height and measure. Once you decided what size works best, use it as your base size for the modular scale. 一旦你决定在你的主体中使用什么字体，你就需要找出什么尺寸最适合。正如我们之前看到的，不是所有的字体尺寸都是一样的。有些看起来更高或更大，有些则更短、更轻。把它放在你的浏览器中，试验一下尺寸、行高和量度。一旦你决定了哪种尺寸最合适，就把它作为你的基础尺寸，用于模块化比例。 ###### 2 Choose a scale There’s quite a few to choose from. Explore and compare them a bit. The golden section is probably the most popular. It’s been popular in graphic design and architecture for ages. It’s based on the Fibonacci numbers which produce a pattern that is supposedly present everywhere in the nature and the universe. The one that I found works best for me is the Perfect Fifth with a ratio of 2:3. I find it to be more flexible than the rest. The goal here is to find out what works best for you and come up with your own unique style. 有相当多的比例尺可以选择。探索和比较一下它们。黄金分割可能是最流行的。它在平面设计和建筑领域已经流行了很久。它基于斐波那契数，产生了一种据说在自然界和宇宙中到处存在的模式。我发现最适合我的是比例为2:3的 "完美五"。我发现它比其他数字更灵活。这里的目标是找出最适合你的方法，并提出你自己的独特风格。 ###### 3 Define all your sizes so they match the scale Once you decided which scale you’ll use, you must define all your text sizes by choosing one from the scale. 一旦你决定了你要使用的比例，你必须从比例中选择一个来定义你所有的文字大小。 ```css // 1. Base size and ratio $base: 1.125em; //= 18px $ratio: 1.5; // Perfect Fifth // 2. The formula for modular scale is (ratio^value)*base so we need a power function @function pow($number, $exponent) { $value: 1; @if $exponent > 0 { @for $i from 1 through $exponent { $value: $value * $number; } } @return $value; } // 3. Let's make it simpler to use by combining everything under one roof @function ms($value, $ms-ratio: $ratio, $ms-base: $base){ $size: pow($ms-ratio, $value)*$ms-base; @return $size; } h1 { font-size: ms(3); // = 60.75px } ``` All we need to use modular scale in a preprocessor like Sass is a couple of variables and functions. Each modular scales breaks down into a single number. 1.5 for the Perfect Fifth, for example. So we save that to the variable $ratio. The other variable we need is the base font size. This needs to match the size of your body font. It’s 18px in this example so I set it to 1.125em. 在像Sass这样的预处理器中，我们所需要的是几个变量和函数来使用模块化刻度。每个模块化音阶都分解成一个数字。例如，1.5为完美五度。所以我们把它保存在变量$ratio中。我们需要的另一个变量是基本字体大小。这需要与你的主体字体的大小相匹配。在这个例子中，它是18px，所以我把它设置为1.125em。 *(ratio^value)\*base ##### Example | **Elements** | **Size** | | -------------- | -------- | | Heading 1 | 3.797em | | Heading 2 | 2.531em | | Heading 3 | 1.668em | | Heading 4 | 1em | | Figure caption | 0.75em | | Small | 0.5em | * #### How to Slow the Ageing of Your Brain https://medium.com/mind-cafe/slow-brain-ageing-heres-how-978073a71604 Our brains start to[ shrink](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2596698/#:~:text=It has been widely found,age particularly over age 70.) around the age of forty. As shrinkage speeds up, our memory, perception, learning, and attention begin to degrade. It becomes harder to form complex thoughts, memorise long sequences, or solve technical problems. But not all experience this drop in brainpower at the same rate. Some people stay sharp as they age, others not so much. ##### A Healthy Gut - Drink plenty of water throughout the day. - Maintain good dental hygiene. - Set a regular schedule for meals. - Eat a wide range of plant-based food. - Keep an active lifestyle: daily walks, aerobics, and so forth. ##### Learning Complex Skills Speaking more than one language[ slows](http://onlinelibrary.wiley.com/doi/10.1002/ana.24158/abstract) cognitive decline and lowers the risk of dementia. Practising a skill stimulates the growth of neurons and promotes neuroplasticity — the brain’s ability to make new neural pathways. Needless to say, learning does wonders for the brain. But not all learning is equal. In a study[ published](http://pss.sagepub.com/content/early/2013/11/07/0956797613499592.abstract?papetoc) in *Psychological Science*, researchers split adults aged sixty to ninety into two groups. They made the first group learn complex skills, such as digital photography, while the second group learned more basic activities, such as crossword puzzles. After ninety days only, the “complex skill” group made surprising gains to their short and long-term memory. In contrast, these gains were absent from the “simple skill” group. These results show that skills that challenge you and get you out of your comfort zone are the most rewarding to your brain. Examples would be learning foreign languages, musical instruments, programming, drawing, sculpture, and choreography. ### 一点收获 - **1rem = 16px** no matter where you set it (unless you changed the font-size of <html>) `rem` means Root `em` - **Mathematics is a language**, and that we can learn it like any other, including our own. --How to read a book. - **About Philosophy**: There are questions not only about being and becoming, but also about necessity and contingency; about the material and the immaterial; about the physical and the non-physical; about freedom and indeterminacy; about the powers of the human mind; about the nature and extent of human knowledge; about the freedom of the will. --How to read a book. - **The Circle Of Fifths** - 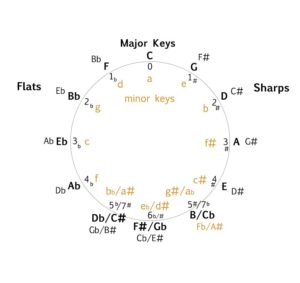 - 7 semitones → Major, 3 semitones → Minor - Right Side: C(0) → G(1♯)→D(2♯)... fa♯.... - Left Side: C(0) → F(1♭)→B♭(2♭)... si♭.... - CDEFGAB → ハニホヘトイロ